X 2 Y 2 Z 2
Tentukan semua tripel bilangan bulat (x, y, z) yang memenuhi sistem persaman : x(y + z) = y^2 + z^2 - 2 y(z + x) = z^2 + x^2 - 2 z(x + y) = x^2 + y^2 - 2
1. Tentukan semua tripel bilangan bulat (x, y, z) yang memenuhi sistem persaman : x(y + z) = y^2 + z^2 - 2 y(z + x) = z^2 + x^2 - 2 z(x + y) = x^2 + y^2 - 2
Dari ketiga bentuk tersebut, coba amati
x(y + z) = y² + z² - 2
xy + xz = (y-1)(y+1) + (z² - 1)
(xy + y) + xz = (y-1)(y+1) + (z² - 1) + y
y(x+1) + xz = (y-1)(y+1) + (y-1) + z²
y(x+1) + xz = (y-1)(y+2) + z²
y(x+1) + xz = (y-1) (y+2) + z² agar kasus menyempit karena z ∈ Z maka z = 0
y(x+1) = (y-1) (y+2) .......................................................(*)
Selanjutnya jumlahkan semua persamaan dan diperoleh
2(x+y+z)² = 6 ( xy + xz + yz + 1)
mengingat x + y + z = 0 , maka
0 = 6 ( x(y+z) + yz + 1)
0 = -x² + yz + 1
x² - 1 = yz dengan x,y,z ∈ Z
(x-1)(x+1) = yz . Jelas untuk x ∈ Z maka solusi x = {-1,1} sehingga
hal itu akan terwujud jika y = 0 atau z = 0.
Untuk y = 0, sehingga tercipta pasangan (x,y,z) = (1,0,z) dan (-1,0,z) dan apabila dimasukkan ke sistem akan diperoleh (x,y,z) = (1,0,-1) dan (-1,0,1)
Untuk z = 0, sehingga tercipta pasangan (x,y,z) = (1,y,0) dan (-1,y,0) dan apabila dimasukkan ke sistem akan diperoleh (x,y,z) = (1,-1,0) dan (-1,1,0).
Begitu pula, berlaku untuk x = 0, sehingga tercipta pasangan (x,y,z) = (x,1,-1) dan (x,-1,1) dan apabila dimasukkan ke sistem akan diperoleh (x,y,z) = (0,-1,1) dan (0,1,-1).∴ Jadi pasangan (x,y,z) = {(-1,1,0) ; (1,-1,0) ; (-1,0,1) ; (1,0,-1) ; (0,1,-1) ; (0,-1,1)}
ada 6 pasang
_________________
Solver : Budi Utomo
_________________
2. x^2 - (y-z)^2/(x+z)^2 - y^2 + y^2 -(x-z)^2/(x+y)^2 - z^2 + z^3 -(x-y)^2/(y+z)^2 - x^2 lebih gampang dilihat dari foto. mohon bantuannya yajangan ngasal
sayakurangyakin maaf
3. (x+y)(z+x+y)=120 (y+z)(y+z+x)=96 (z+x)(x+y+z)=72 nilai dari x^2+y^2+z^2 adalah....
Diketahui persamaan (x + y)(z + x +y)=120 , (y + z)(y + z + x)=96 , (z + x)(x + y + z)=72 maka nilai dari x² + y² + z² = 13
PendahuluanSistem Persamaan Linear Tiga Variabel Atau yang sering disingkatdengan SPLTVmerupakan konsep Persamaan yang melibatkan variabel sebanyak 3 biasanya berupa x,y,dan z.
Metode yang bisa digunakan untuk menyelesaikan Bentuk PLTV :
Metode Substitusi yaitu dengan menyamadengankan salah satu variabel.Metode Eliminasi yaitu dengan menjumlahkan ataupun mengurangkan persamaan yang satu dengan yang lainnya, sehingga akan menghilangkan salah satu variabel untuk mempermudah mencari penyelesaian.Metode MatrikMetodeDeterminan PembahasanDari soal diketahui[tex]\begin{cases}(x+y)(z+x+y)=120~...\green{\text{Persamaan~1}}\\ (y+z)(y+z+x)=96~...\green{\text{Persamaan~2}} \\ (z+x)(x+y+z)=72~... \green{\text{Persamaan~3}}\end{cases}[/tex]
Ditanya :[tex]x^2+y^2+z^2=[/tex]
Langkah-langkah penyelesaian :»Dari ketiga persamaan buatlah sebuah perbandingan
•Dari persamaan 1 dan 2
[tex]\frac{(x+y)\cancel{(z+x+y)}}{(y+z)\cancel{(y+z+x)}} &=& \frac{120}{96} \\ \frac{(x+y)}{(y+z)} &=& \frac{5}{4}~...\green{\text{Persamaan~4}}[/tex]
•Dari persamaan 2 dan 3
[tex]\frac{(y+z)\cancel{(y+z+x)}}{(z+x)\cancel{(x+y+z)}} &=& \frac{96}{72} \\ \frac{(y+z)}{(z+x)} &=& \frac{4}{3}~...\green{\text{Persamaan~5}}[/tex]
»Diperoleh Persamaan 4 dan 5
[tex]\begin{cases}\frac{(x+y)}{(y+z)} &=& \frac{5}{4}~...\green{\text{Persamaan~4}} \\ \\ \frac{(y+z)}{(z+x)} &=& \frac{4}{3}~...\green{\text{Persamaan~5}}\end{cases}[/tex]
»Persamaan 4 dan 5 dipersingkat menjadi
[tex]\begin{cases}x+y=5~...\green{\text{Persamaan~A}} \\ y+z=4~...\green{\text{Persamaan~B}} \\ z+x=3~...\green{\text{Persamaan~C}} \end{cases}[/tex]
»Dari Persamaan A Diperoleh
[tex]x+y &=& 5 \\ \red{x} &=& 5-y~...\green{\text{Persamaan~D}}[/tex]
»Substitusi x diatas ke Persamaan yang mengandung variabel x selain A yaitu persamaan C
[tex]z+x &=& 3 \\ z+(5-y) &=& 3 \\ \red{z} &=& y-2~...\green{\text{Persamaan~E}}[/tex]
Menentukan masing-masing variabel»Variabel y (Substitusikan Persamaan E ke Persamaan B)
[tex]y+z &=& 4 \\ y+(y-2)&=& 4 \\ 2y &=& 6[/tex]
[tex]\large{\blue{\boxed{y=3}}}[/tex]
»Variabel x (Substitusikan y = 3 ke Persamaan A)
[tex]x+y &=& 5 \\ x+3 &=& 5 \\ x &=& 5-3[/tex]
[tex]\large{\blue{\boxed{x=2}}}[/tex]
»Variabel z (Substitusikan x = 2 ke Persamaan C)
[tex]x+z &=& 3 \\ 2+z &=& 3 \\ z &=& 3-2[/tex]
[tex]\large{\blue{\boxed{z=1}}}[/tex]
»Diperoleh Himpunan Penyelesaian
[tex]HP~{(x=2),(y=3),(z=1)}[/tex]
Ditanya :[tex]\Large{x^2+y^2+z^2 =}[/tex]
Jawab :[tex]x^2+y^2+z^2=2^2+3^2+1^2[/tex]
[tex]x^2+y^2+z^2=4+9+1[/tex]
[tex]\Large{\boxed{x^2+y^2+z^2=13}}[/tex]
KesimpulanJadi nilai dari x²+y²+z² yang memenuhi persamaan diatas adalah 13
Pelajari lebih lanjutDefinisi dan Contoh Soal PLTV : https://brainly.co.id/tugas/6594911Menentukan Hasil Penyelesaian SPLTV : https://brainly.co.id/tugas/25110557Contoh soal SPLTV lainnya… : https://brainly.co.id/tugas/11562466Detail JawabanMapel : Matematika Wajib
Kelas : X
Materi : Sistem Persamaan Linear Tiga Variabel (Bab 2)
Kode Kategorisasi : 10.2.2 (Kelas 10,Kode mapel 2)
Kata Kunci : Menentukan jumlah kuadrat semua variabel
©ekoanswer™
4. Tentukan hasil dari x,y,z yang memenuhi sistem X+y+z=2 X-y+z=2 X-y-z=2
Jawaban:
~ Mathx + y + z = 2
x - y + z = 2
x - y - z = 2
x + y + z = 2
x - y + z = 2
__________ _
2y = 0
y = 0
x + y + z = 2
x - y - z = 2
_________ _
2y + 2z = 0
2(0) + 2z = 0
2z = 0
z = 0
x + y + z = 2
x + 0 + 0 = 2
x = 2
Hp {2 , 0 , 0}
5. jika x = 1/2 y z = 2 y maka x + y berapa z
x : y = 1 : 2
y : z = 1 : 2
x + y = ...z?
2y+y =...z?
3y=....z?
3*1/2 = 3/2z
............................................ x3+y3+z3-3xyz=1/2(x+y+z)((x-y)2+(y-z)2+(z-x)2)
Equation is alway trueRearrange:Rearrange the equation by subtracting what is to the right of the equal sign from both sides of the equation :
x^3+y^3+z^3-3*x*y*z-(1/2*(x+y+z)*((x-y)^2+(y-z)^2+(z-x)^2))=0
Step by step solution :Step 1 :Simplify (x-y)2 + (y-z)2 1.1
Evaluate : (x-y)2 = x2-2xy+y2 1.2 Evaluate : (y-z)2 = y2-2yz+z2
Equation at the end of step 1 : 1 ((((x3)+(y3))+(z3))-3xyz)-((—•(x+y+z))•((x2-2xy+2y2-2yz+z2)+(z-x)2)) = 0 2 Step 2 :
Simplify x2-2xy+2y2-2yz+z2 + (z-x)2 2.1
Evaluate : (z-x)2 = z2-2xz+x2
Equation at the end of step 2 : 1 ((((x3)+(y3))+(z3))-3xyz)-((—•(x+y+z))•(2x2-2xy-2xz+2y2-2yz+2z2)) = 0 2 Step 3 : x+y+z
Multiply ————— by 2x2-2xy-2xz+2y2-2yz+2z2 2
6. 3. Perhatikan bentuk berikut (x + y + z) ^ 2 = x ^ 2 + y ^ 2 + z ^ 2 + 2(xy + yz + xz)x + y + z = 7x ^ 2 + y ^ 2 + z ^ 2 = 9x × y × z = 51/x + 1/y + 1/z =?Lebih jelasnya ada di foto ya
Jawaban:
4
Penjelasan dengan langkah-langkah:
[tex](x + y + z) ^ 2 = x ^ 2 + y ^ 2 + z ^ 2 + 2(xy + xz + yz) \\ {(7)}^{2} = 9 + 2(xy + xz + yz) \\ 49 = 9 + 2(xy + xz + yz) \\ 40 = 2(xy + xz + yz) \\ \frac{40}{2} = xy + xz + yz \\ xy + xz + yz = 20[/tex]
[tex] \frac{1}{x} + \frac{1}{y} + \frac{1}{z} = \frac{yz + xz + xy}{xyz} \\ = \frac{xy + xz + yz}{xyz} \\ = \frac{20}{5} \\ = 4[/tex]
7. [tex]{(2 - x)}^{2} + {(y - 2)}^{2} + {(z + 2)}^{2} = { - z}^{2} + {y}^{2} - {x}^{2} + 2(x - z + y)[/tex]sederhanakan plis.
Jawaban:
2z² – 6(x + y – z) + 12 = 0
Penjelasan dengan langkah-langkah:
semoga terhibur
8. Jika z=arc tg x/y , buktikan (∂^2 z)/∂x∂y=(∂^2 z)/∂y∂x Jika z=ln〖(x-a)^2 〗+(x-b)^(2 )tujukan bahwa (∂^2 z)/〖∂x〗^2 +(∂^2 z)/〖∂y〗^2 =0 kecuali titika (a,b) Jika z=f(x+ay)-g(x-ay) tunjukan bahwa (∂^2 z)/〖∂x〗^2 =1/a^2 ×(∂^2 z)/〖∂y〗^2 jikaz=x^n f(x/y) tenjukan x ∂z/∂x+y ∂z/∂y=n z jika z=e^(-kn^2 t) sinnx buktikan bahwa ∂z/∂x=k (∂^2 z)/〖∂x〗^2
Saya bantuin beberapa saja y
Nomor 1 :
[tex]z=\arctan{\frac{y}{x}}[/tex]
Tunjukkan [tex]\frac{\partial^2{z}}{\partial{x}\partial{y}}=\frac{\partial^2{z}}{\partial{y}\partial{x}}[/tex]
Kita harus mencari turunan parsial dari bentuk tersebut.
Ingat, turunan dari y = arctan f(x) adalah :
[tex]y'=\frac{f'(x)}{1+{f(x)}^{2}}[/tex]
Dengan rumus ini, kita juga bisa mencari turunan dari soal tersebut.
[tex]\frac{\partial^{2}{z}}{\partial{x}\partial{y}}=\frac{\frac{x-y}{x^2}}{1+\frac{y^2}{x^2}}\\\frac{\partial^{2}{z}}{\partial{x}\partial{y}}=\frac{x-y}{x^2+y^2}\\\frac{\partial^{2}{z}}{\partial{y}\partial{x}}=\frac{x-y}{x^2+y^2}[/tex]
Pada dasarnya [tex]\frac{\partial^2{z}}{\partial{x}\partial{y}}[/tex] dengan [tex]\frac{\partial^2{z}}{\partial{y}\partial{x}}[/tex] adalah sama hanya berbeda saat memulainya.
Jadi,
[tex]\frac{\partial^2{z}}{\partial{x}\partial{y}}=\frac{\partial^2{z}}{\partial{y}\partial{x}}[/tex] (terbukti)
Untuk sementara segitu dulu.
9. x+y+z=22x+y+2z=23x-y-z=2maka x+y+z...
Jawaban:
2
Penjelasan dengan langkah-langkah:
Lihat di persamaan yang pertama yaitu : x+y+z=2 berarti x+y+z adalah 2
10. X^2+y^2=z^2, tentukan x,y dan z
[tex]x^2 + y^2 = z^2 [/tex]
[tex]x^2+y^2-z^2=0[/tex]
[tex]x^2 = z^2 - y^2[/tex]
[tex]x = \sqrt{z^2-y^2} [/tex]
[tex]y^2 = z^2 - x^2[/tex]
[tex]y = \sqrt{z^2-x^2} [/tex]
[tex]z^2 = -x^2-y^2[/tex]
[tex]z = \sqrt{-x^2-y^2} [/tex]
Maaf ya kalo salah
11. 1/x + 2/y - 1/z = 32/x + 1/y + 2/z = 72/x - 2/y - 2/2 = 2Tentukan nilai x, y, dan z adalah
Jawaban:
y:4 x:5 z:8...............
12. (x+y)2 =.... (x-y+z)2 =... (x+y-z)2=.... *note: 2= kuadrat
(x+y)2 = x2+y2
(x-y+z)2 = x2-y2+z2
(x+y-z)2 = x2+y2-z2
2 = kuadrad
( x + y )^2
= ( x + y )( x + y )
= [tex] x^{2} + xy + xy + y^{2} [/tex]
= [tex] x^{2} + 2xy + y^{2} [/tex]
( x - y + z )^2
= ( x - y + z )( x - y + z )
= [tex] x^{2} - xy + xz - xy + y^{2} - yz + xz - yz + z^{2} [/tex]
= [tex] x^{2} - 2xy + 2xz + y^{2} - 2yz + z^{2} [/tex]
( x + y + z )^2
= ( x + y + z )( x + y + z )
= [tex] x^{2} + xy +xz + xy + y^{2} + yz + xz + yz + z^{2} [/tex]
= [tex] x^{2} + 2xy + 2xz + y^{2} + 2yz + z^{2} [/tex]
semoga membantu^^
13. Tentukan hasil dari x,y,z yang memenuhi sistem X+y+z=2 X-y+z=2 X-y-z=2
eliminasi x dari pers 1 Dan 2
x+y+z=2
x-y+z=2
2y=0
y=-2
eliminasi z dari pers 2 dan 3
x-y+z=2
x-y-z=2
2x=4
x=2
substitusi x=2, y=-2, ke pers 1
x+y-z=2
2-2-z=2
z=-2
jadi x=2, y=-2, z=-2
14. [tex] {(2 - x)}^{2} + {(y - 2)}^{2} + {(z + 2)}^{2} = { - z}^{2} + {y}^{2} - {x}^{2} + 2(x - z + y)[/tex]sederhanakan plis.
Jawaban:
2(z² – 3[x + y – z] + 6) = 0Penjelasan dengan langkah-langkah:
semoga membantu ^^
15. Diketahui : X - Y + Z = - 4 2 X + Y + 2 Z = - 5 3 X - Y - Z = - 6 maka nilai dari 2 X - 3 Y - 2 Z adalah
2X - 3Y - 2Z = (-4) * 2 + (-5) * (-3) + (-6) * (-2)
= -8 -15 +12
= -11
menggunakan metode eliminasi untuk menyelesaikan sistem persamaan di atas. Pertama, kalikan persamaan pertama dengan 2, persamaan kedua dengan -3, dan persamaan ketiga dengan -2. Kemudian, tambahkan hasil perhitungan tersebut untuk mendapatkan persamaan baru.
16. x(x+y+z)=a^2 y(x+y+z)=b^2z(x+y+z)=c^2tentukan nilai x,y,z
x,y,dan z nilainya sama gak.kalo sama nilai x,y dan z 1
17. 2 x + 5 Y + 2 Z + 4 x y + 2 y z + 5 x y z
Jawaban:
9x8y2z
Penjelasan dengan langkah-langkah:
2x + 5y + 2z + 4xy + 2yz + 5xyz
= (2x + 4x + 5x) (5y + y + 2y + y) (z + z)
= 9x8y2z
maaf jika salah
semoga membantu
[tex]2x + 5y + 2z + 4xy + 2yz + 5xyz \\ pertama - tama \: kita \: klompookan \: yg \: sejenis \\ 2 + 5 + 2 + 4 + 2 + 5 + x + x + x + y + y + y + y + z + z + z \\ 20 x ^{3} y {}^{4} z {}^{3} [/tex]
Semoga bermanfaat ^_^
18. Tentukan hasil dari x,y,z yang memenuhi X+y+z=2 X-y+z=-2 X-y-z=2
(1)-(2)
2y = 4
y = 2
(1)+(3)
2x = 4
x = 2
2-2-z = 2
-z= 2
z = -2
19. 3. Tentukan penyelesaian dari2 x - y+z=-1X + y - z=-23 x + 2 y +z=2
Jawaban:
Penjelasannya ada di gambar
20. hasil dari X Y memenuhi sistem X + Y + Z =2 X -Y+Z= -2 X-Y-Z = 2 adalah?
(I) x + y + z = 2
(II) x - y + z = -2
---------------------- -
2y = 4
y = 2
(I) x + 2 + z = 2
x + z = 0
(III) x - 2 - z = 2
x - z = 4
x + z = 0
x - z = 4
------------- -
2z = -4
z = -2
x + y + z = 2
x + 2 - 2 = 2
x = 2
Video Update
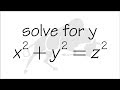 Reviewed by Franco
on
June 16, 2022
Rating:
Reviewed by Franco
on
June 16, 2022
Rating:
Post a Comment